La conosci e la sapresti scrivere? Tutto quello che c’è da sapere su questa formula che ha molto a che fare con la natura
La sequenza di Fibonacci è un enigma matematico affascinante che ha affascinato gli studiosi per secoli. Essa è chiamata “la formula perfetta” perché appare in molti aspetti della natura, dall’arte e l’architettura alla biologia e alla tecnologia.
Cos’è la sequenza di Fibonacci?
La sequenza di Fibonacci è una serie di numeri che inizia con 0 e 1, e ogni numero successivo è la somma dei due numeri precedenti. In altre parole, la sequenza inizia con 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, e così via, all’infinito. Questa serie è stata coniata da Leonardo Fibonacci, un matematico italiano del XIII secolo, ma la sequenza era conosciuta in India molto prima di lui.
Chi era Fibonacci
Leonardo di Pisa, meglio noto come Fibonacci, è famoso per aver introdotto in Europa il sistema numerico indo-arabo, noto come sistema decimale posizionale, che è oggi ampiamente utilizzato in tutto il mondo. La sua opera più celebre è il libro “Liber Abaci” (Il libro dell’abaco), scritto nel 1202, in cui introdusse questo sistema numerico e illustrò la sua applicazione pratica.
Fibonacci nacque a Pisa intorno al 1170 ed è stato educato in Nord Africa, dove suo padre lavorava come commerciante. Durante il suo soggiorno in Nord Africa, Fibonacci apprese il sistema numerico indo-arabo e riconobbe il suo enorme potenziale. Quando tornò in Italia, iniziò a scrivere il “Liber Abaci” per diffondere questa nuova conoscenza. Il “Liber Abaci” conteneva una serie di concetti matematici avanzati, tra cui l’aritmetica, la geometria e le proporzioni, nonché problemi matematici pratici riguardanti il commercio, le conversioni di valute e le equazioni di interesse. Tuttavia, la parte più significativa del libro fu l’introduzione dei numeri arabici (1, 2, 3, ecc.) e del concetto di zero come sistema numerico di base.
Il sistema numerico indo-arabo sostituì gradualmente il sistema numerico romano precedentemente utilizzato in Europa, poiché risultava molto più efficiente per calcoli matematici complessi. L’opera di Fibonacci ebbe un impatto duraturo sulla matematica europea e aprì la strada per lo sviluppo della matematica moderna.
Fibonacci morì intorno al 1250, ma la sua eredità matematica continua a influenzare la disciplina matematica e la cultura matematica in tutto il mondo.
La formula perfetta della natura
La sequenza di Fibonacci è considerata la “formula perfetta” della natura per diversi motivi. Uno dei modi più evidenti in cui appare in natura è attraverso il rapporto aureo, noto anche come “phi” (φ). Questo rapporto è definito dalla seguente equazione:
φ = (1 + √5) / 2
Il rapporto aureo è approssimativamente uguale a 1,61803398875. Questo numero rappresenta una proporzione che è considerata esteticamente piacevole e armoniosa. È ampiamente utilizzato in architettura, arte e design, poiché le forme e le proporzioni che seguono il rapporto aureo sono spesso percepite come visivamente gradevoli. Molte opere d’arte e edifici famosi, come la Gioconda di Leonardo da Vinci e il Partenone ad Atene, seguono queste proporzioni.
Ma la sequenza di Fibonacci non si ferma qui. Si trova anche in molti aspetti della biologia, come la disposizione dei petali dei fiori, le spire di una chiocciola, la disposizione delle foglie lungo un ramo e molto altro. Questo modello si riflette perfettamente in molte strutture naturali, rendendolo un esempio di come la matematica sia intrecciata con il mondo naturale.

Un’altra proprietà interessante è che i numeri consecutivi di Fibonacci sono coprimi, il che significa che non hanno fattori comuni. Inoltre, il prodotto di quattro numeri consecutivi è approssimativamente uguale al quadrato del numero aureo, cioè (φ^2 ≈ 2,61803398875).
La sequenza di Fibonacci in tecnologia e finanza
La sequenza di Fibonacci è stata utilizzata anche in tecnologia e finanza. Ad esempio, i trader di mercato finanziario spesso studiano i livelli di supporto e resistenza basati su questa sequenza per prendere decisioni sugli investimenti. Inoltre, è utilizzata nella progettazione di algoritmi e nella crittografia.
La geometria e la sequenza di Fibonacci
Un aspetto affascinante della sequenza di Fibonacci è la sua connessione con la geometria. I rettangoli che seguono le proporzioni della sequenza di Fibonacci sono noti come “rettangoli d’oro” o “rettangoli aurei”. Se disegni una serie di rettangoli d’oro e li raccordi in un’armoniosa spirale, otterrai una spirale che somiglia alle spire di una chiocciola.
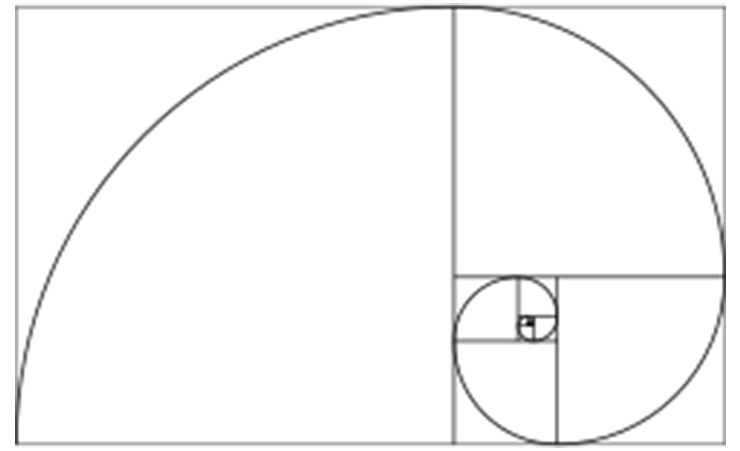
Questa spirale, nota come “spirale aurea” o “spirale di Fibonacci”, è una delle forme più ricorrenti in natura.
La sequenza di Fibonacci e la musica
La connessione tra la sequenza di Fibonacci e la musica è affascinante e rivelatrice. La matematica e la musica sono due discipline che possono sembrare distinte, ma ci sono molte sovrapposizioni e intersezioni, e la sequenza di Fibonacci offre un esempio di come la matematica possa influenzare la creazione musicale.
La sequenza di Fibonacci, insieme al rapporto aureo, può essere applicata alla musica in vari modi:
Durate e Ritmi: Le durate delle note musicali possono seguire una sequenza di Fibonacci. Ad esempio, la durata di una nota potrebbe essere 1, quella della nota successiva 1, quella della terza nota 2, poi 3, 5, 8, ecc. Questo schema può creare ritmi e strutture ritmiche complesse e interessanti.
Struttura Compositiva: I compositori hanno utilizzato la sequenza di Fibonacci per guidare la struttura delle loro composizioni. Le parti musicali possono essere organizzate in base a questa sequenza, con sezioni di lunghezze diverse in accordo con i numeri di Fibonacci.
Temi Melodici: Alcuni compositori hanno utilizzato la sequenza di Fibonacci per creare temi melodici. Ad esempio, potrebbero comporre una melodia che segue il pattern della sequenza, utilizzando il numero di Fibonacci per determinare l’altezza delle note o l’intervallo tra le note.
Strumentazione: La sequenza di Fibonacci può anche essere applicata alla scelta degli strumenti musicali utilizzati in una composizione. Ad esempio, un compositore potrebbe pianificare l’uso di strumenti diversi in base a questa sequenza, creando una varietà di suoni e timbri.
Strutture Armoniche: La sequenza di Fibonacci può essere utilizzata per creare strutture armoniche complesse e interessanti. Le progressioni armoniche possono essere guidate da questa sequenza, contribuendo a creare un suono armonioso e bilanciato.
L’eredità della sequenza di Fibonacci
La sequenza di Fibonacci e il rapporto aureo continuano a ispirare artisti, matematici, scienziati e designer in tutto il mondo. Essi sono un esempio straordinario di come la matematica sia intrinsecamente legata alla bellezza e all’armonia che osserviamo in natura e nell’arte. La sequenza di Fibonacci ci ricorda che, anche dietro ciò che sembra caotico e casuale, può esserci una profonda struttura matematica che dà vita a un mondo di bellezza e perfezione.
La sequenza di Fibonacci è un’affascinante espressione matematica che si manifesta in modo così pervasivo nella natura, nell’arte e nella scienza. La sua bellezza e armonia la rendono un esempio di come la matematica sia intrinsecamente collegata al nostro mondo. Questa “formula perfetta” continua ad ispirare e stupire gli studiosi e gli appassionati di tutto il mondo, dimostrando che la bellezza matematica è una forza universale.
Può interessarti anche: “Quanti anni ha l’universo?”






